Gerçekten oldu mu?

Evet.

Japon Hitomi uzay aracının başarısızlığının araştırılması dönmekte olduğunu ortaya çıkardı tutum kontrol hatası nedeniyle çok hızlı. Sonuç olarak, uzay aracı o kadar hızlı döndü ki birkaç parça enkaz kaydedildi.

Ancak buna tepki tekerleri değil iticiler neden oldu.

Paralel olarak @Heopps yanıtı:

Gerçekten oldu mu?

Evet.

Muhteşem bir şekilde!

1965'te NASA, Fırlatma Kaçış Sistemini (LES) test etmek için Little Joe II roketinde standart bir Apollo komuta modülü başlattı ve beklediklerinden daha fazla test yaptı. Jiroskopların hatalı bir şekilde takılması nedeniyle, kanatçıkların üzerindeki kontrol kanatları fırlatma sırasında tam sapmaya gitti ve roketin dönmesine neden oldu, öyle ki merkezkaç kuvveti katı motorlar için motor yuvalarını kırdı ve roket LES'in başlatması gereken irtifa. Bu uçuşun videosu çok güzel!

İstenmeyen uçuş profiline rağmen, LES gerçek iptal durumu.

Bu örneğin bir uzay aracını içermediğine dikkat edin, çünkü bu test Karman hattına hiç ulaşmadı ve ulaşması amaçlanmadı ve sadece standart bir komut modülü kullandı. @Heopps cevabı sizi gerçek bir uzay aracının talihsiz ölümüne yönlendiriyor.

EDIT 2018 Temmuz 2018

Dönen uyluk kemiğine hitap etmek için gerçek bir uyluk kemiği çok daha fazlasıdır bir silindirden daha karmaşık.

Ama önce, engin fizik okyanusuna sadece ayak parmağını (şimdiye kadar!) batırmış biri için iyi bir deneme yaptığınızı söyleyeyim! Birçoğunun beyni bir denklem görür görmez donacaktı, ama siz yapmadınız. Aferin sana!

Silindir hesaplamasıyla ilgili olarak, bu nesnenin kütle merkezi etrafında döndüğünü unutmayın. Tüm kütlenin silindirin uçlarında yoğunlaştığını varsayarsanız (ki bu elbette değildir, ancak şimdilik bunu varsayalım), 125 gramlık iki kütle 25 cm dönme yarıçapıyla dönüyor demektir. Dönen kütle ve dönme yarıçapının 250 gm ve 50 cm olması için, çubuğun merkezin değil bir ucunun etrafında dönmesi ve tüm kütlenin diğer uçta olması gerekir. Bunun yerine 25 cm'lik bir dönme yarıçapı ile dönen 125 gm'lik iki kütleye sahibiz, böylece denklem V = SQRT (4kN * 0.25m / 0.125kg) = 89.44 m / s veya ~ 3400 RPM olur. (Bu, 4 kN'nin nihai bir gerilme gücü olduğunu varsayar) Bu aslında hesaplamanızın belirttiğinden daha hızlıdır ! Bu denklem, 125 gm'lik kütlelerden yalnızca birinin uyguladığı kuvveti hesaplar: diğeri aynı kuvveti tam tersi yönde uygulayacaktır, bu nedenle bunlardan yalnızca birini hesaplamak yeterlidir.

Bir varsayarsak kütlesinin uzunluğu boyunca eşit olarak dağıldığı gerçek ince silindir, silindirin dönme eksenine yakın olan kısımları uçlardan daha yavaş bir hızda hareket eder, bu nedenle uçlarda olmalarına göre daha az merkezkaç kuvveti üretirler. Orta noktada üretilen net gerilim, kütlenin uçlarda yoğunlaştığı durumun yarısı kadardır ( değil !), Böylece gerçekte √ çarpanıyla daha hızlı dönebilirsiniz. 2.

Gerçek femurlar, tek tip silindir ile yukarıdaki durum arasında ortada bir yerde, kütlenin tamamen uçlarda yoğunlaştığı, ancak bir komplikasyon var.

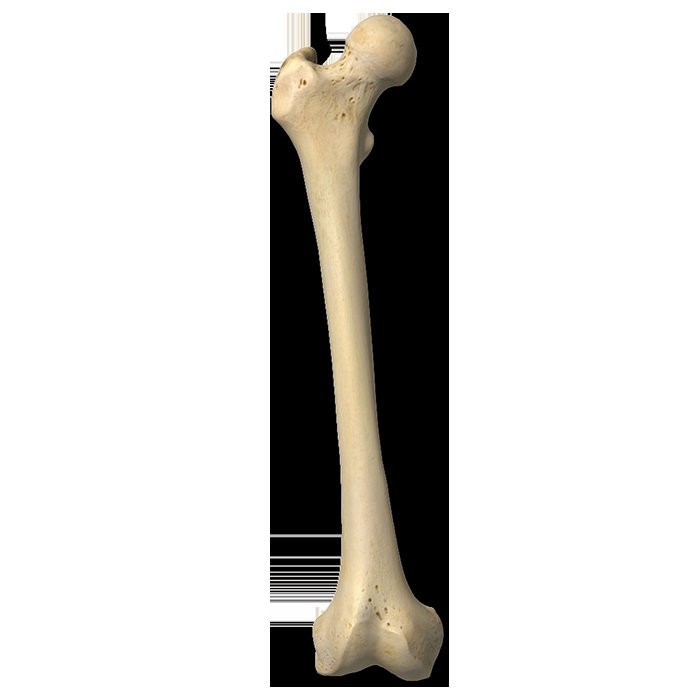
Komplikasyon, görüntüden de görebileceğiniz gibi, uyluk kemiğinin silindirik olarak simetrik olmaması. Homojen bile değil. Üst ("proksimal") uçta bir tarafa uzanan önemli bir kütle parçası ( Gray'in Anatomisi 'ne göre baş ) vardır. Ve burada gösterilmese de şaft genellikle düz değildir ve kemik homojen değildir, bu nedenle yerel kütle yoğunlukları sabit değildir. Dönerken asimetri, tamamen çekme gerilimine ek olarak (@ TheNate, gerilimi ilgili birincil metrik olarak doğru bir şekilde tanımlamıştır) şafta uygulanan bir eğilme momentinin olduğu anlamına gelir. Şaftın belirli bir enine kesitinde (örneğin, kütle merkezinde) bu eğilme momenti bir taraftaki gerilimi azaltır ve diğer tarafta arttırır. Kemikte önceden var olan çatlakların olmadığı varsayıldığında, ilk kırılma artan gerilimin meydana geldiği ve tüm şaft boyunca Griffith çatlağı olarak hızla yayıldığı yerde meydana gelir. Bu, yukarıda hesaplanandan daha yavaş bir dönüş hızında gerçekleşebilir.

Tepki çarkı? Hayır, bunlar KSP'de fazlasıyla güçlendirilmiştir ve gerçek uzay araçlarında neredeyse yüksek tork uygulamazlar, doygunluk sorununu (reaksiyon çarkı motorunun maksimum hızı) boşverin.

Ancak asimetrik itme kesin bir şeydir. Tehlike. Bir roketin bazı motorları ateşlenemezse veya ateş etmeyi erken durdurursa, geri kalanlar onu bir dönüşe gönderecektir. Ve bu gerçekten kötü bitebilir. Üstelik sadece çıkışta değil - yörüngede sıkışmış bir RCS iticisi de aynı derecede kötü haber.

Evet, kesinlikle.

Dönen, rijit bir yapının her parçası, dönme ekseninin yarıçapı ve açısal hızın karesiyle orantılı olarak merkeze doğru ivmeye maruz kalır. Bu teknik olarak merkezcil kuvvettir, ancak potansiyel olarak yapı ile bağlantısı kopabilecek bir cismin yerel çevresinde, dönen bir çerçevede dışa doğru bir kuvvet olarak ele alınabilir, bu nedenle genellikle merkezkaç kuvveti.

Kuvvet dönme ekseninden gelen yarıçapla arttığından, uzay aracının en dıştaki parçaları en fazla kuvvete maruz kalır; her şey eşit derecede güvenli bir şekilde bağlanırsa, önce en dıştaki bitler düşer.

Parçalar düştüğünde, bağlantı kesildikleri anda sahip oldukları anlık hız ile, yani dönme yarıçaplarına teğet bir doğru üzerinde hareket edeceklerdir. Dönen referans çerçevesinde, böyle bir parçanın düşmeden önce içinde bulunduğu, bu düz yol yaklaşık olarak parabolik görünür; hareket, yerçekimine bağlı ivmeye çok benzer.

Bu kuvvetin etkisi prensipte yolcuların yararına dönen bir uzay aracındaki yerçekimini simüle etmek için kullanılabilir, ancak bu amaçla daha büyük bir yarıçap ve daha yavaş bir dönüş kullanmak tercih edilir Coriolis etkisi.

Kerbal Space Program'ın yapısal bağlantıları genellikle gerçek hayattaki uzay araçlarından daha güçlüdür, ancak oyun içinde dönen bir gemiden bazı şeyleri düşürebileceğinize inanıyorum.

(SF., bir aracı reaksiyon çarkları ile muhtemelen reaksiyon çarkları dışında herhangi bir şeye zarar verecek kadar hızlı döndüremeyeceğiniz konusunda doğru.)

Bir uzay aracı, kendisini parçalayacak kadar hızlı dönebilir mi? Buna hangi kuvvet neden olur (eğer öyleyse) ve hangi kısımlar bu kuvvete en çok duyarlıdır?

Bu, ona neden olan bir kuvvet meselesi değil, bir kuvvet eksikliği kadar . Newton'un Birinci Yasasına göre, bir cisim üzerine bir kuvvet uygulanmadıkça sabit hızda kalır. Hız hem hızı hem de yönü içerdiğinden, sabit hızda hareket eden bir nesne ya sabittir ya da düz bir çizgide hareket eder.

Bir nesne için (bir uzay gemisinin parçası gibi) ) Dairesel bir yolda ilerlemek için, bu yolun merkezine doğru sürekli olarak hızlandırılması gerekir. Newton'un Birinci Yasası, üzerine bir kuvvet etki etmedikçe bunun mümkün olmadığını söyler. Newton'un İkinci Yasası bize bu kuvvetin nesnenin kütlesinin ivmesi ile çarpımına eşit olduğunu söyler.

Dönen bir nesne örneğinde, uzay aracının dış kısımlarını tutan parça bir kuvvet uygulamaktadır. uzay aracının merkezine doğru yönlendirilen dış kısımlara. Dönme hızı, bu dış kısımları dairesel bir yolda tutmak için gereken ivmenin, dış nesnenin kütlesine bölünmesinin sağlayabileceği maksimum kuvvetin üzerine çıktığı noktaya kadar arttığında, parça dış nesneyi tutar. başarısız olur ve dışarıdaki nesne düz bir çizgide uçar.

Nuclear Wang'ın bir yorumda bahsettiği gibi, aynı davranışı bir ipteki topla da gözlemleyebilirsiniz. Topu ipin üzerinde döndürdüğünüzde, ip, dönüşün merkezine doğru topa bir kuvvet (gerginlik denir) uygular. Topu bu dairesel yolda tutmak için gereken ivmenin topun kütlesine bölünerek sağlayabileceği maksimum gerilim kuvvetine ulaşacak kadar hızlı döndürdüğünüzde, ip kopacak ve top uçacaktır. Hava sürtünmesi ve Dünya'nın yerçekimi (aynı zamanda topa etki eden kuvvetler) olmasaydı, top düz bir çizgide uçardı.

Muhtemelen bununla ilgili bir sorun, xkcd şöhretine sahip Randall Monroe'nun NASCAR yarışını tamamlamanın en hızlı yolu hakkındaki What If makalesinde incelediği bir sorundur:

https: //what-if.xkcd. com / 116 /

Makalenin ikinci yarısında, merkezi bir nokta etrafında dönen bir sistemi anlatıyor. Bu spin hızının sınırı, eğirme yapan malzemenin kopma mukavemetidir. Alakalı girişi alıntılamak için (her şeyi ve arşivin geri kalanını okumanızı tavsiye ederim. İyi şeyler!):

Kevlar kayışlarla bağlanmış bir "araç" hayal edin diğer tarafta bir karşı ağırlık ile güçlendirilmiş merkezde bir pivot. Aslında, bu dev bir santrifüj. Bu, en sevdiğim tuhaf denklemlerden birini uygulamamıza izin veriyor, şöyle diyor: dönen bir diskin kenarı, yapıldığı malzemenin özgül mukavemetinin (çekme mukavemetinin yoğunluğa bölünmesi) karekökünden daha hızlı gidemez . Kevlar gibi güçlü malzemeler için bu hız 1-2 km / sn'dir. Bu hızlarda, bir kapsül muhtemelen yarışı yaklaşık 10 dakikada bitirebilir - ancak kesinlikle içeride yaşayan bir sürücü olmasa da.

Sizin durumunuzda soru şu oluyor: bir içindeki hangi yapısal malzeme uzay gemisi en düşük özgül güce sahip mi? Dönme gerilimi nedeniyle başarısız olduğunda, muhtemelen her şey başarısız olacaktır.

Sorunun dönüş ekseniyle ilgili olduğunu görüyorum. Uçtan uca, uzun bir silindirin nasıl dönmeyi 'istediği' dir. Bu konuda, uzunlukları etrafında dönmeyen ilk uydularla ilgili sorunları vardı, çünkü malzemedeki herhangi bir bükülme, momemtum'u uçtan uca yuvarlanma rotasyonuna aktaracaktı. Dönme momentumu arttıkça, aktarılacak daha fazla momentum olur ve malzemenin mükemmel sertliğinden herhangi bir sapma büyür. Üst ve alt sallanmaya başlayacaktı.

Ve bükülmeden yuvarlanmaya geçtiğinde, kuvvet ve sıcaklık farklılıkları onu çabucak parçalara ayırır.

Bu bir tür kural. Buna karşı aktif önlemler almalısınız. Bir geminin katı çerçevesine sabitlenmiş bir noktadan, ağırlık merkezine tam olarak işaret edilmeyen herhangi bir sürekli ivme / itme, ağırlık merkezi etrafında bir dönüşe neden olacak ve ivmenin devam etmesi, dönüş miktarını artıracaktır. Uzayda doğal bir sınır veya frenleme yoktur. Hafifletici bir faktör, kararlı rotasyon modlarının yalnızca en büyük ve en küçük özdeğerlere karşılık gelen eylemsizlik tensörünün özvektörleri ile ilgili olmasıdır: bu rotasyon modları diğer eksenlere bozunamaz. Ancak iki sabit dönme ekseni etrafında dönmeye devam eden herhangi bir katkı birikecek ve katıyı bir arada tutan ortaya çıkan merkezcil kuvvetler sonunda herhangi bir malzemeyi kıracaktır.